CJ's Notebook

Why 0.1 + 0.2 ≠ 0.3? Floating Numbers in JavaScript

Published on
#JavaScript

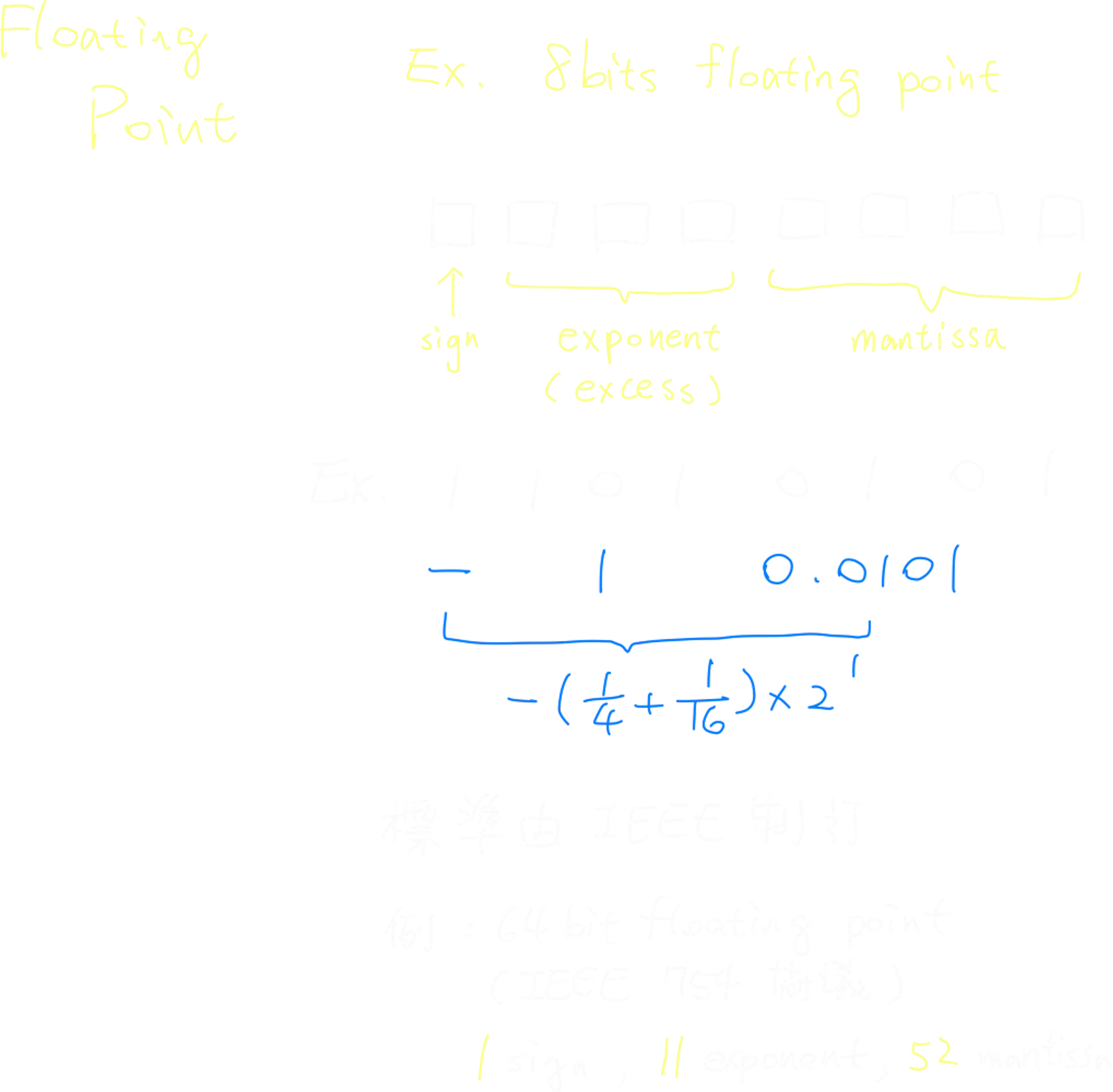
In JavaScript, all numbers are stored in the format of IEEE-754 double precision numbers. The numbers are stored in binary form with 1 bit sign, 11 bits exponent, and 52 bits mantissa.

Floating point

When converting decimal numbers into binary form, not all decimal values have exact binary correspondence. These values are rounded to their most accurate representation to be stored.

In the context of IEEE-754 double precision numbers, “round” means approximating a real number with the nearest representable floating-point number.

When a rounded value is added or subtracted by another rounded value, the result might be different from the rounded value of the calculation of original value.

For example, round(0.1) + round(0.2) is not equal to round(0.3),

General Form

sign=1→−sign=0→}(1.mantissa)2×2(exponent−1023)10\begin{rcases} \text{sign=1} \rightarrow - \\ \text{sign=0} \rightarrow \end{rcases} (1.mantissa)_2\times{2^{(exponent-1023)}}_{10}
  • Sign: 1 or 0
  • Exponent: 0 to 2110 \ to \ 2^{11}
    • 0 to 210→(−210+1) to −10\ to\ 2^{10} \rightarrow (-2^{10} + 1)\ to\ -1
    • 210+1→02^{10}+1 \rightarrow 0
    • (210+2) to 211→1 to (210−1)(2^{10}+2)\ to\ 2^{11} \rightarrow 1\ to\ (2^{10}-1)
    • Exponents range from −1022 to +1023 because exponents of −1023 (all 0s) and +1024 (all 1s) are reserved for special numbers (0 and Infinity).
  • Mantissa: 1.xxxxxxxx...xxxxxxxx⏞Mantissa: 52 bits, x = 1 or 02{1.\overbrace{\text{xxxxxxxx...xxxxxxxx}}^{\text{Mantissa: 52 bits, x = 1 or 0}}}_2

Example: 2048=2¹¹

  • Sign: 0
  • Exponent: 11
    • 11+1023=1034
    • in binary: 10000001010210000001010_2
  • Mantissa: 2
    • in binary: 00…00 (all zeros)

Example: Largest Number

  • Sign: 0
  • Exponent: 1023
    • 111111111102=(211−2)1011111111110_2=(2^{11}-2)_{10}
    • (211−2)−(210−1)=210−1=1023(2^{11}-2)-(2^{10}-1)=2^{10}-1=1023
  • Mantissa: 1111…111 (all ones)

value=1.1111...111⏞52 bits2×2102310=1111...111⏞53 bits2×21023−52=971=(253−1)×2971=21024−2971\text{value}={1.\overbrace{1111...111}^{\text{52 bits}}}_2\times{2^{1023}}_{10}={\overbrace{1111...111}^{\text{53 bits}}}_2\times2^{1023-52=971}=(2^{53}-1)\times2^{971}=2^{1024}-2^{971}

  • This is the Number.MAX_VALUE

Example: Largest Safe Integer

(“Safe” in this context refers to the ability to represent integers exactly and to compare them correctly.)

A safe integer is an integer that:

  • can be exactly represented as an IEEE-754 double precision number, and
  • whose IEEE-754 representation cannot be the result of rounding any other integer to fit the IEEE-754 representation.
  • Sign: 0
  • Exponent: 52 (limited by Mantissa numbers of bit)
  • Mantissa: 11111…111 (all ones)

value=1.111111...111⏞52 bits2×25210=111...111⏞53bits2=253−1\text{value}={1.\overbrace{111111...111}^{\text{52 bits}}}_2 \times {2^{52}}_{10}={\overbrace{111...111}^{\text{53bits}}}_{2}=2^{53}-1

  • This is the Number.MAX_SAFE_INTEGER

Example: +0 (Special Case)

  • Sign: 0
  • Exponent: 00000000000
  • Mantissa: 0000…000 (all zeros)

original value=1.0000...000⏞52 bits2×2−102310=2−1023\text{original value}={1.\overbrace{0000...000}^{\text{52 bits}}}_2 \times {2^{-1023}}_{10}=2^{-1023} cannot be represent

Example: 0.1

  • Sign: 0
  • Exponent: (1023−4)10=011111110112(1023-4)_{10}=01111111011_2
  • Mantissa: 1001100110011001100110011001100110011001100110011010
Most accurate representation=1.10011001100...110011010⏞52 bits2×2−410=0.100000000000000005551115123126\begin{align*} \text{Most accurate representation}&={1.\overbrace{10011001100...110011010}^{\text{52 bits}}}_2 \times {2^{-4}}_{10}\\ &=0.100000000000000005551115123126 \end{align*}
  • But why the engine display 0.1? —> The engine only display the necessary precision that can distinguish different binary numbers.

Example: 0.2

  • Sign: 0
  • Exponent: (1023−3)10=011111111002(1023-3)_{10}=01111111100_2
  • Mantissa: 1001100110011001100110011001100110011001100110011010
Most accurate representation=1.10011001100...110011010⏞52 bits2×2−310=0.200000000000000011102230246252\begin{align*} \text{Most accurate representation}&={1.\overbrace{10011001100...110011010}^{\text{52 bits}}}_2 \times {2^{-3}}_{10}\\ &=0.200000000000000011102230246252 \end{align*}

Example: 0.3

  • Sign: 0
  • Exponent: (1023−2)10=011111111012(1023-2)_{10}=01111111101_2
  • Mantissa: 0011001100110011001100110011001100110011001100110011
Most accurate representation=1.0011001100...1100110011⏞52 bits2×2−210=0.299999999999999988897769753748\begin{align*} \text{Most accurate representation}&={1.\overbrace{0011001100...1100110011}^{\text{52 bits}}}_2 \times {2^{-2}}_{10}\\ &=0.299999999999999988897769753748 \end{align*}

Example: 0.1 + 0.2

0.1ac=0.00011001100110011001100110011001100110011001100110011010⏞56 bits2\text{0.1ac}={0.\overbrace{00011001100110011001100110011001100110011001100110011010}^{\text{56 bits}}}_2

0.2ac=0.0011001100110011001100110011001100110011001100110011010⏞55 bits2\text{0.2ac}={0.\overbrace{0011001100110011001100110011001100110011001100110011010}^{\text{55 bits}}}_2

0.1ac+0.2ac=0.010011001100...110011001110⏞56 bits2\text{0.1ac+0.2ac}={0.\overbrace{010011001100...110011001110}^{\text{56 bits}}}_2

0.1ac+0.2ac=0.010011001100...110011001110⏞56 bits2=1.0011001100...110011001110⏞54 bits2×2−210(need rounding to 52bits)=1.0011001100...1100110100⏞52 bits2×2−210=0.300000000000000044408920985006=0.30000000000000004\begin{aligned} \text{0.1ac+0.2ac}&={0.\overbrace{010011001100...110011001110}^{\text{56 bits}}}_2\\ &=1.{\overbrace{0011001100...110011001110}^{\text{54 bits}}}_2 \times {2^{-2}}_{10} \text{(need rounding to 52bits)} \\ &=1.{\overbrace{0011001100...1100110100}^{\text{52 bits}}}_2 \times {2^{-2}}_{10}\\ &=0.300000000000000044408920985006\\ &=0.30000000000000004 \end{aligned}